📐 Matrices

✏️ Definición De Matrices

Una matriz es un arreglo bidimensional de números, símbolos o elementos dispuestos en filas y columnas. Cada elemento en una matriz se encuentra ubicado en una posición específica definida por su fila y columna. Las matrices se utilizan en diversas ramas de las matemáticas, la física, la informática y muchas otras disciplinas para representar y manipular datos de manera organizada y eficiente.

¿Como crear una matriz en python?

Para crear una matriz en python se debe importar la libreria numpy y luego crear un arreglo de numpy con los datos de la matriz.

Creación de una matriz en python

import numpy as np
matriz = np.array([[1,2,3],[4,5,6],[7,8,9]])
#Aqui estamos creando una matriz de 3x3 los componentes de la matriz son los números del 1 al 9
tambien podemos usar
matriz1=np.random.random((3,3))
#Aqui estamos creando una matriz de 3x3, esto lo especificamos en el parentesis, especificamos cuantas columnas y filas queremos respectivamente. Los componentes de la matriz son números aleatorios entre 0 y 1

🛠️ Algunos métodos de matrices con numpy

Las matrices que manejamos en NumPy, por ser justamente arreglos bidimensionales, cuentan con prácticamente las mismas funcionalidades de los arreglos convencionales. De esta forma es que, por ejemplo, podemos hacer uso de indexing para acceder a un determinado elemento (pudiendo ser éste un dato o inclusive una lista) y de slicing para poder extraer un rango de datos.

Indexing y slicing en matrices

import numpy as np
matrix = np.arange(15, dtype=np.int64).reshape((3,5))
        array([[ 0,  1,  2,  3,  4],
       		   [ 5,  6,  7,  8,  9],
       		   [10, 11, 12, 13, 14]], dtype=int64)
matrix[1,3] # = matrix[1][3]
	     8
matrix[0, 1:3]
	    array([1, 2], dtype=int32)

** Ahora si empecemos con los metodos de matrices **

1️⃣ Método .max()

Este método nos permite encontrar el valor máximo de una matriz.

Encontrar el valor maximo de una matriz

import numpy as np
matriz = np.array([[1,2,3],[4,5,6],[7,8,9]])
matriz.max()

☝🏽 Pero tambien lo podemos usar de otra manera.

Ya que este método permite el ingreso de otro argumento, y el cual vendría siendo un valor que define el eje de la matriz para el cual se van a obtener los valores máximos.

Encontrar el valor maximo de una matriz con eje

import numpy as np
x = np.arange(15, dtype=np.int64).reshape((3,5))
	    array([[ 0,  1,  2,  3,  4],
       		   [ 5,  6,  7,  8,  9],
       		   [10, 11, 12, 13, 14]], dtype=int64)
np.max(x, axis = 0)
	    array([ 10, 11, 12, 13, 14])

Con el eje ‘0’ obtenemos de vuelta el número máximo por columnas. Mientras que con el eje ‘1’ obtenemos como resultado el número máximo por filas.

Encontrar los valores maximos de una matriz por columnas y filas

import numpy as np
np.max(x, axis = 1)
        array([ 4, 9, 14])
        #Aqui estamos encontrando los valores maximos de la matriz por filas, mientras que en el ejemplo anterior encontramos los valores maximos de la matriz por columnas

2️⃣ Método .min()

Este método nos permite encontrar el valor mínimo de una matriz.

Encontrar el valor minimo de una matriz

import numpy as np
matriz = np.array([[1,2,3],[4,5,6],[7,8,9]])
matriz.min()

3️⃣ Método .shape

Este atributo de la clase de las matrices nos permite encontrar las dimensiones (número de columnas y de filas) de una matriz.

Encontrar las dimensiones de una matriz

import numpy as np
matriz = np.array([[1,2,3],[4,5,6],[7,8,9]])
matriz.shape

4️⃣ Método .zeros()

Este método nos permite crear una matriz de ceros. Tenemos que especificar las dimensiones de la matriz.

Crear una matriz de ceros

import numpy as np
matriz = np.zeros((3,3))
#Aqui estamos creando una matriz de 3x3, esto lo especificamos en el parentesis, especificamos cuantas columnas y filas queremos respectivamente. Los componentes de la matriz son ceros

5️⃣ Método .ones()

Este método es parecido al anterior, pero en vez de crear una matriz de ceros, crea una matriz de unos.

Crear una matriz de unos

import numpy as np
matriz = np.ones((3,3))
#Aqui estamos creando una matriz de 3x3, esto lo especificamos en el parentesis, especificamos cuantas columnas y filas queremos respectivamente. Los componentes de la matriz son unos

6️⃣ Método random.random()

Este método nos permite crear una matriz de números aleatorios entre 0 y 1. Tenemos que especificar las dimensiones de la matriz.

Crear una matriz de números aleatorios entre 0 y 1

import numpy as np
matriz = np.random.random((3,3))
#Aqui estamos creando una matriz de 3x3, esto lo especificamos en el parentesis, especificamos cuantas columnas y filas queremos respectivamente. Los componentes de la matriz son números aleatorios entre 0 y 1

7️⃣ Método .random.randint()

Este método nos permite crear una matriz de números aleatorios entre 0 y otro número entero. Tenemos que especificar las dimensiones de la matriz.

Crear una matriz de números aleatorios entre 0 y otro número entero

import numpy as np
matriz = np.random.randint(10, size=(3,3))
#Aqui estamos creando una matriz de 3x3, esto lo especificamos en el parentesis, especificamos cuantas columnas y filas queremos respectivamente. Los componentes de la matriz son números aleatorios entre 0 y 10

8️⃣ Método .random.seed()

Para entender este metodo tenemos que entender que en la programación no hay una aleatoriedad completa, sino más bien es una pseudo aleatoriedad, y por ello la semilla se utiliza para plantear el patrón de aleatoriedad. Y este método que sirve para inicializar una serie de números supuestamente aleatorios, mismo que puede llegarse a ocupar en matrices.

Crear una matriz de números

import numpy as np
np.random.seed(123)
matriz = np.random.randint(10, size=(3,3))
#Aqui estamos creando una matriz de 3x3, esto lo especificamos en el parentesis, especificamos cuantas columnas y filas queremos respectivamente. Los componentes de la matriz son números aleatorios entre 0 y 10

9️⃣ Método .where()

El método where() nos permite encontrar los índices de los elementos de una matriz que cumplan una condición. Por ejemplo:

Encontrar los indices de los elementos de una matriz que cumplan una condición

import numpy as np
matriz = np.array([[1,2,3],[4,5,6],[7,8,9]])
np.where(matriz>5)
#Aqui estamos encontrando los indices de los elementos de la matriz que sean mayores a 5

Tambien podemos usar otra forma, la cual nos regresa los elementos de la matriz que cumplan la condición.

Encontrar los elementos de una matriz que cumplan una condición

import numpy as np
matriz = np.array([[1,2,3],[4,5,6],[7,8,9]])
matriz[matriz>5]
#Aqui estamos encontrando los elementos de la matriz que sean mayores a 5

🔟 Método .reshape()

Con este método estamos modificando la forma del determinado arreglo sin cambiar sus datos. Para ello, el argumento que le enviamos debe de estar en un iterable (como lo es una tupla) en el cual el primer elemento corresponde al número de filas y el segundo al número de columnas.

Cambiar la forma de una matriz

import numpy as np
np.arange(12, dtype=np.int64).reshape((4,3))
	    array([[0, 1, 2],
       		   [3, 4, 5],
       		   [6, 7, 8],
               [9, 10, 11]], dtype=int64)

De esta forma estamos indicando que la matriz va a tener 4 filas y 3 columnas. Ahora bien, es importante denotar que la nueva forma de la matriz debe de ser tal que pueda tener la misma cantidad de elementos que la forma original.

1️⃣1️⃣ Método .mean()

Este método permite saber el promedio numérico de los datos de la matriz con base a un eje en específico.

Encontrar el promedio de los datos de una matriz

import numpy as np
x = np.arange(15, dtype=np.int64).reshape((3,5))
	    array([[ 0,  1,  2,  3,  4],
       		   [ 5,  6,  7,  8,  9],
       		   [10, 11, 12, 13, 14]], dtype=int64)
x.mean(axis = 0)
	     array([ 5, 6,  7, 8, 9])

1️⃣2️⃣ Método .linspace()

El respectivo método nos da muestras numéricas en un incremento o decremento uniforme con base a un intervalo. El primer argumento que recibe es el valor de inicio, el segundo es el valor donde termina, y el tercero es la cantidad de muestras.

Crear un arreglo de muestras numéricas en un incremento o decremento uniforme

import numpy as np
np.linspace(0, 8, 5)
         array([ 0., 2., 4., 6., 8.])

1️⃣3️⃣ Método .arange()

Este método nos arroja un arreglo con base en un rango de números.

Crear un arreglo con base en un rango de números

import numpy as np
np.arange(10)
	    array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
        #Aqui estamos creando un arreglo de 10 elementos, los cuales son números del 0 al 9

Ahora bien, este método acepta otro argumento que permite definir el tipo de dato que se va a guardar en el determinado arreglo.

Crear un arreglo con base en un rango de números con tipo de dato especifico

import numpy as np
np.arange(10, dtype=np.float32)
	    array([ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9.], dtype=float32)

🌟 ¿Qué es dtype?

En este sentido, con dtype podemos definir dicho tipo de dato, y para lo cual en el ejemplo mostrado, ahora cada dato se guarda como un float de 32 bits. Cabe destacar que el tipo de dato aplica para todos los datos del arreglo o matriz, ya que para un arreglo en Python es fundamental que todos los datos sean del mismo tipo.

🤔 Conceptos basicos de matrices

Una matriz se compone por filas y columnas, las cuales se pueden representar de la siguiente manera: n: Número de filas, m: Número de columnas. Por lo tanto nXm nos da el tamaño de la matriz.

📚 Tipos de Matrices

Existen diferentes tipos de matrices, las cuales se clasifican según su forma y sus elementos. A continuación se presentan los tipos de matrices más comunes:

1️⃣ Matriz fila

La Matriz fila es una matriz muy sencilla ya que se compone de solamente una fila. Aunque puede tener N columnas. Por ejemplo:

Creación de una matriz Fila en python

import numpy as np
matriz = np.array([[1,2,3]])
tambien podemos usar
matriz1=np.linspace(1,10,3) #Aqui estamos creando una matriz de 1x3, esto lo especificamos en el parentesis, especificamos cuantas columnas y filas queremos respectivamente. Los componentes de la matriz son números aleatorios entre 0 y 1

2️⃣ Matriz columna

Igualmente la Matriz Columna es muy sencilla ya que se compone de solamente una columna. Aunque puede tener N filas. Por ejemplo:

Creación de una matriz Columna en python

import numpy as np
matriz = np.array([[1],[2],[3]])

3️⃣ Matriz cuadrada

Las Matrices Cuadradas son aquelllas que tienen el mismo número de filas que de columnas. (n=m) Por ejemplo:

Creación de una matriz Cuadrada (3x3) en python

import numpy as np
matriz = np.array([[1,2,3],[4,5,6],[7,8,9]])

4️⃣ Matriz rectangular

Las matrices rectangulares son aquellas que tienen diferente número de filas que de columnas. (n!=m) Por ejemplo:

Creación de una matriz Rectangular(2x3) en python

import numpy as np
matriz = np.array([1,2,3],[4,5,6])

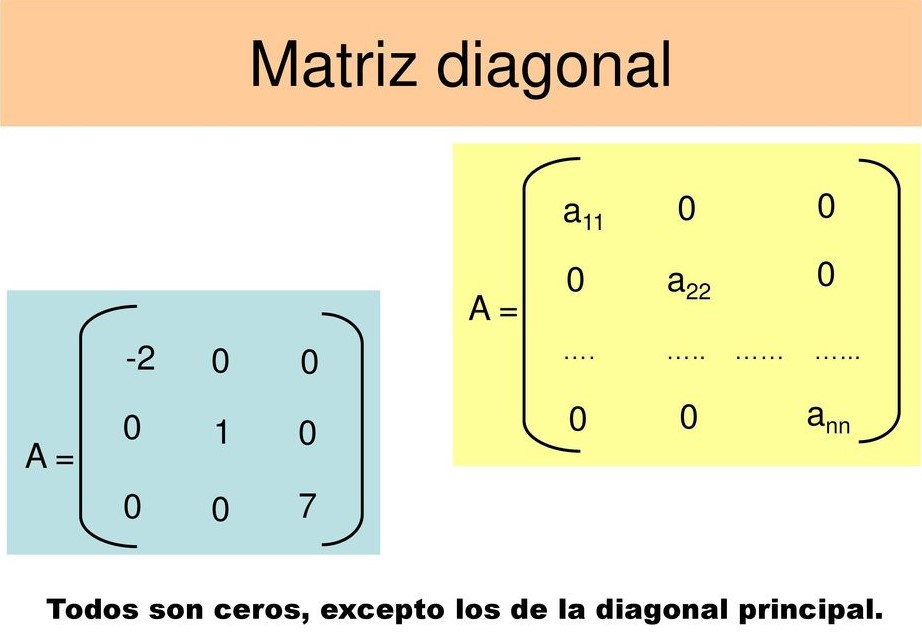
5️⃣ Matriz diagonal

Las Matrices Diagonales son aquellas que tienen todos sus elementos fuera de la diagonal principal iguales a cero. Por ejemplo:

6️⃣ Matriz Unidad (identidad)

La Matriz Identidad es una matriz cuadrada que tiene todos sus elementos de la diagonal principal iguales a 1 y los demás elementos iguales a cero. Por ejemplo:

Creación de una matriz identidad(3x3) en python

import numpy as np
matriz = np.identity([1,2,3],[4,5,6],[7,8,9]) #Creación matriz identidad (3x3)
matriz1= np.eye(3) #Creación matriz identidad (3x3)

☝🏽️ Matrices triangulares

Las Matrices triangulares son aquellas que tienen todos sus elementos por encima o por debajo de la diagonal principal iguales a cero. Existen dos tipos de Matrices triangulares: Matriz Triangular Superior y Matriz Triangular Inferior.

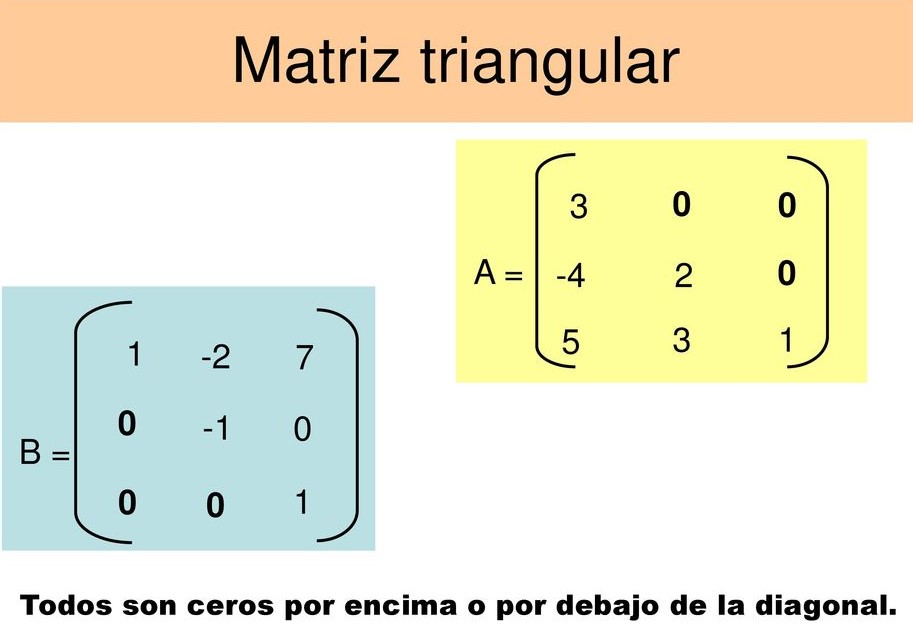
7️⃣ Matriz triangular superior

La Matriz Triangular Superior es aquella que tiene todos sus elementos por debajo de la diagonal principal iguales a cero.

8️⃣ Matriz triangular inferior

La Matriz Triangular Inferior es aquella que tiene todos sus elementos por encima de la diagonal principal iguales a cero.

En la siguiente imagen se muestran los dos tipos de matrices triangulares:

9️⃣ Matriz transpuesta

La Matriz transpuesta de cualquier matriz es aquella que se obtiene al cambiar las filas por las columnas de una matriz. Por ejemplo:

Creación de una matriz transpuesta en python

import numpy as np
matriz = np.array([1,2,3],[4,5,6],[7,8,9])#Creación matriz (3x3)
Hay dos formas de trasponer la matriz:
matrizTraspuesta = matriz.T #Creación matriz traspuesta (3x3)
matrizTraspuesta=matriz.transpose() #Creación matriz traspuesta (3x3)

Hay mas tipos de matrices, pero esto no es curso de Álgebra Lineal. 😅